[Home] AI로 돌아가기
ReLU (Rectified Linear Unit) 함수 (렐루 함수)
ReLU(Rectified Linear Unit) 함수는 딥러닝에서 가장 많이 사용되는 활성화 함수 중 하나다. 입력이 0보다 크면 그대로 출력하고, 0 이하이면 0을 출력하는 방식으로 작동한다.
목차
1. 배경
- 렐루 함수는 딥러닝 역사에 있어 한 획을 그은 활성화 함수인데, 렐루 함수가 등장하기 이전엔 시그모이드 함수를 활성화 함수로 사용해서 딥러닝을 수행했다.
- 그러나, 시그모이드 함수는 출력하는 값의 범위가 0에서 1사이므로, 레이어를 거치면 거칠수록 값이 현저하게 작아지게 되어 기울기 소실(Vanishing gradient) 현상이 발생하였다.
- 이 문제는 1986년부터 2006년까지 해결되지 않았으나, 제프리 힌튼 교수가 제안한 렐루 함수로 인해, 시그모이드의 기울기 소실 문제가 해결되게 되었다.
- 렐루 함수는 우리말로, 정류된 선형 함수라고 하는데, 간단하게 말해서 +/-가 반복되는 신호에서 - 흐름을 차단한다는 의미다.
- 렐루 함수는 은닉층에서 굉자히 많이 사용되는 데, 별생각 없이 다층 신경망을 쌓고, 은닉층에 어떤 활성화 함수를 써야 할지 모르겠다 싶으면, 그냥 렐루 함수를 쓰라고 할 정도로, 아주 많이 사용되는 활성화 함수이다.
2. ReLU 함수란?
ReLU는 "Rectified"(정류된)와 "Linear Unit"(선형 유닛)의 합성어다. "정류"는 교류(AC)를 직류(DC)로 변환하는 개념에서 따온 것으로, ReLU 함수가 음수를 0으로 변환하는 특징과 유사하기 때문에 붙여진 이름이다.
동작 방식:
- 입력 값이 0보다 크면 그대로 출력
- 입력 값이 0 이하이면 0을 출력
3. 수학적 표현
ReLU 함수는 다음과 같이 정의된다.
$$ f(x) = \max(0, x) $$
즉, 입력 \( x \) 가 0보다 크면 그대로 출력하고, 0 이하이면 0을 출력한다.
4. ReLU 함수의 장점
- 기울기 소실(Vanishing Gradient) 문제 완화: 시그모이드 함수나 하이퍼볼릭 탄젠트 함수와 달리, ReLU는 양수 영역에서 기울기가 1이므로 기울기 소실 문제가 줄어든다.
- 계산 효율성: 단순한 max 연산으로 이루어져 있어 계산 속도가 빠르다.
- 희소성(Sparsity): 0 이하의 값이 0으로 변환되므로 일부 뉴런이 비활성화된다. 이는 신경망의 일반화 성능을 높이는 데 기여할 수 있다.
5. ReLU 함수의 한계
- 죽은(ReLU Dying) 문제: ReLU는 입력이 0 이하이면 0을 출력하기 때문에 일부 뉴런이 영구적으로 비활성화될 수 있다.
- 출력값의 비대칭성: 음수 영역이 0이기 때문에 평균 출력값이 0보다 크며, 이를 해결하기 위해 Leaky ReLU, Parametric ReLU(PReLU) 등의 변형이 사용된다.
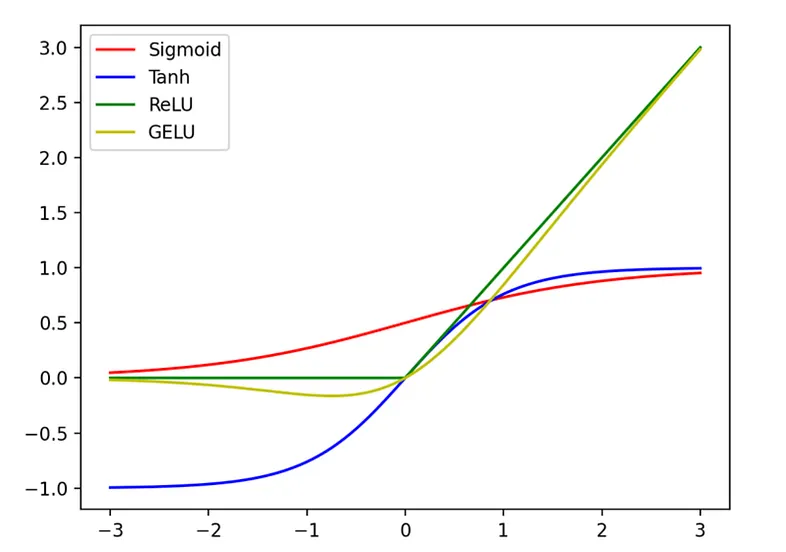 GeLU ~ A smoother ReLU
GeLU ~ A smoother ReLU
출처: https://medium.com/better-ml/relu-vs-gelu-d322422f5147

